Largest Rectangle in Histogram Problem
Given n non-negative integers representing the histogram’s bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.
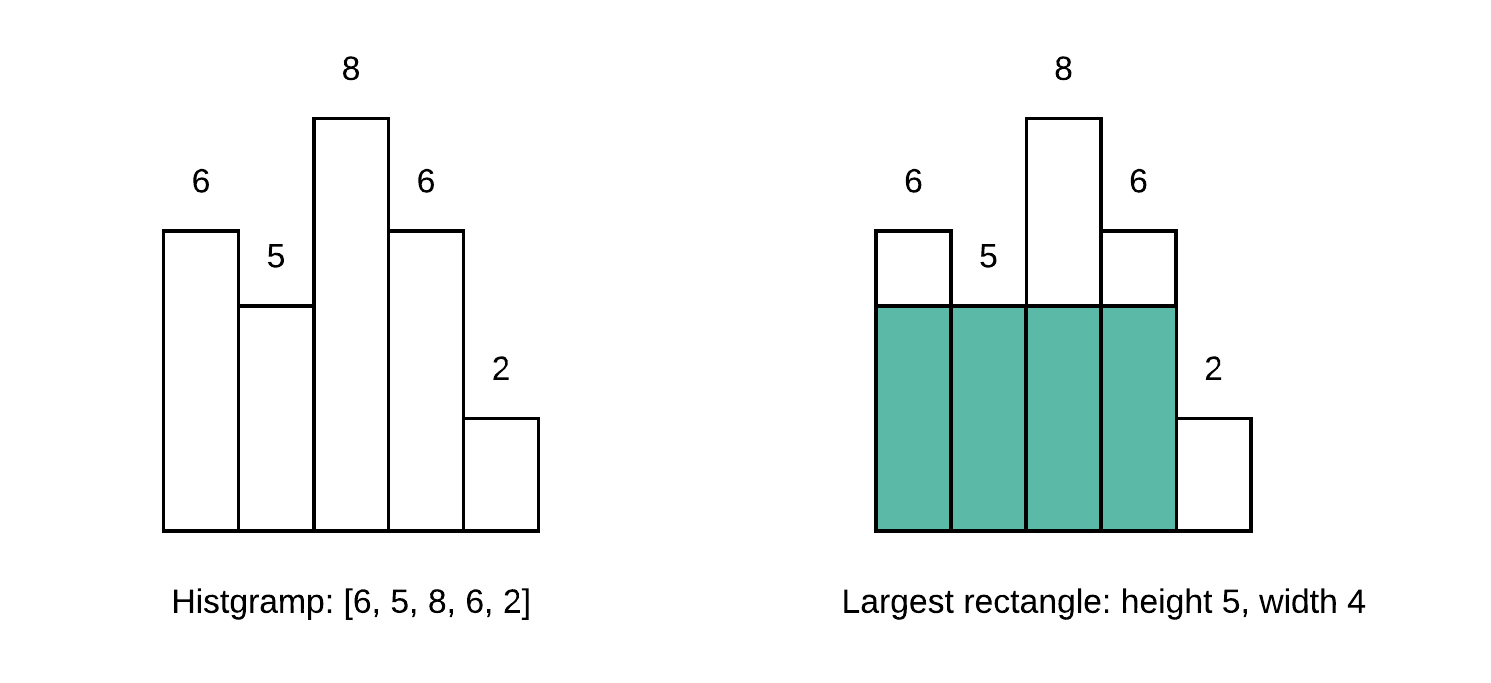
The following is a histogram with the width of bar of 1, and heights of [6, 5,8,6,2].
The largest rectangle is painted in green, which has in total 20 unit.
Max rectangle in histogram
Very similar to what we’ve discussed on Dynamic Programming: Maximal Rectangle, the area of a rectangle is determined by three different dimensions:
- Height
- Left boundary
- Right boundary.
As shown in the following diagrams:
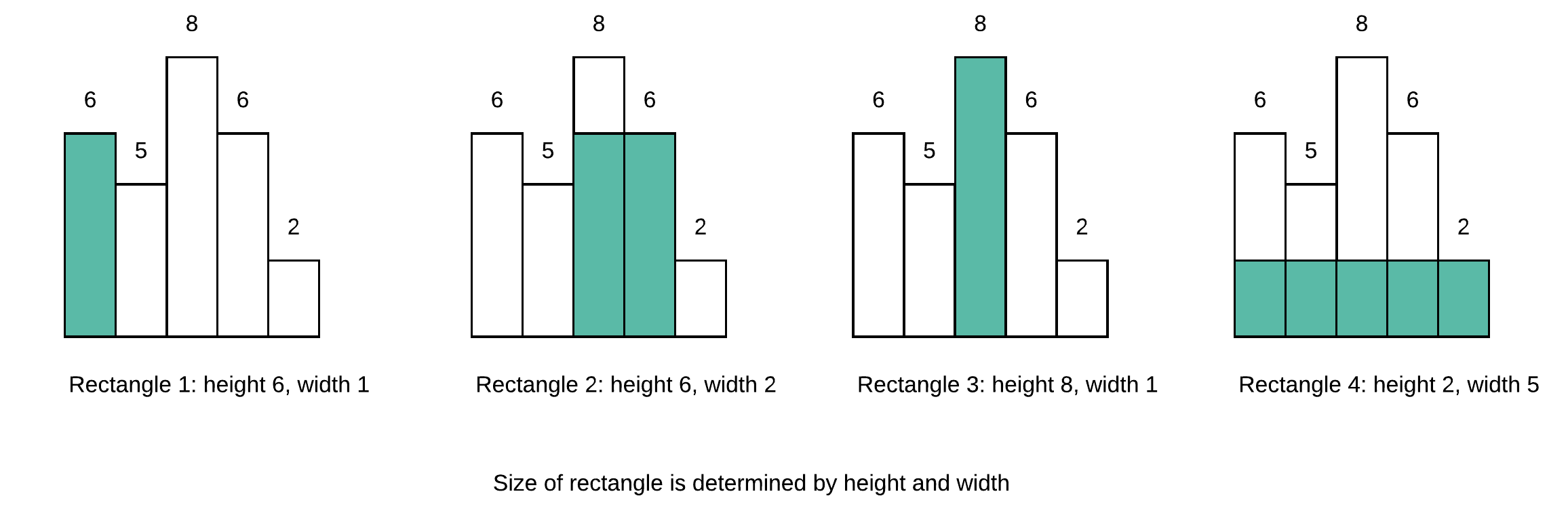
- For each bar i, it can form a rectangle with the height of heights[i]
- Area of this rectangle is determined by left boundary and right boundary
- Max rectangle can be found from one of the rectangles
Left boundary and right boundary
The key question is:
How to find left/right boundary?
By definition:
- left_boundary[i] = j, when height[j, i] >= height[i] and height[j – 1] < height[i]
- right_boundary[i] = k, when height[i, k] >= height[i] and height[k + 1] < height[i]
Which means, the left boundary is the left most index where the bars between it and the current bar are no lower than current bar, while the one left to the left boundary is shorter than current bar.
One simple way to find left/right boundary is to search from index i until you find the first bar lower than height[i], but this solution takes O(n ^ 2), which is too expensive.
To find left/right boundary efficiently, consider the following observation:
- If heights[i] > heights[i – 1], then left(i) = i
- If heights[i] <= heights[i – 1], then left(i) = left(i – 1)
- If heights[i] > heights[i + 1], then right(i) = i
- If heights[i] <= heights[i + 1], then right(i) = right(i + 1)
Combine the latter two with the first two, we got the following algorithm of computing the leftBoundary and rightBoundary:
- Create empty stack
- For each bar 0 ~ n – 1:
- If stack.isEmpty() or heights[i] >= height[stack.peek]
- stack.push(i)
- If !stack.isEmpty() and heights[i] < heights[stack.peek]
- left(stack.peek) = stack.peek, right(stack.peek) = i
- repeat until stack empty or heights[i] >= heights[stack.peek]
- If stack.isEmpty() or heights[i] >= height[stack.peek]
The following example illustrated how the above algorithm works:
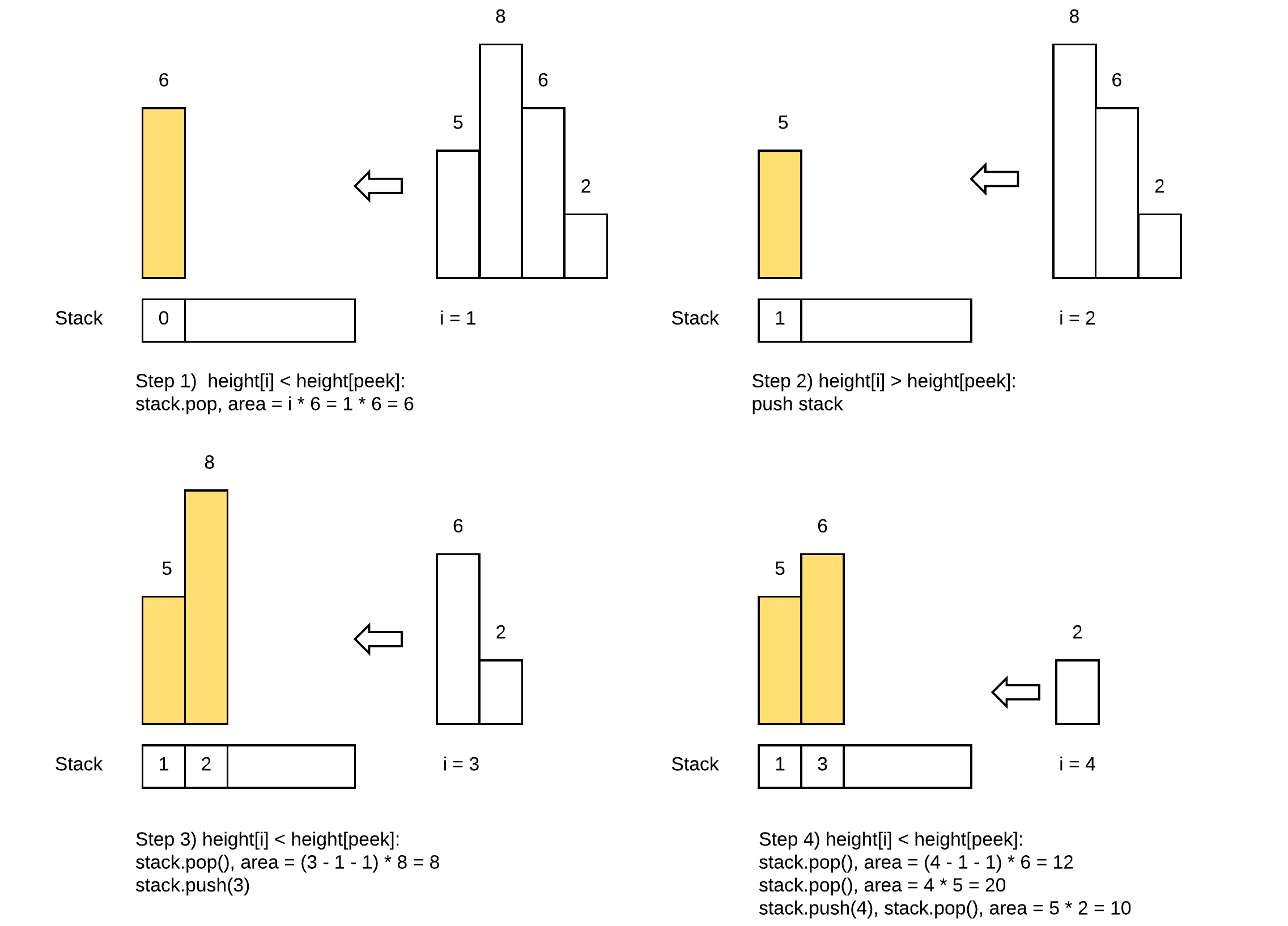
Implementation
The following code implements the algorithm above.
public int largestRectangleArea(int[] heights) {
if (heights == null || heights.length == 0) {
return 0;
}
int maxArea = 0;
int len = heights.length;
Stack stack = new Stack();
for (int i = 0; i<= heights.length; i++) {
while (!stack.isEmpty() && (i == len || heights[stack.peek()] > heights[i])) {
int height = heights[stack.pop()];
int width = stack.isEmpty() ? i : i - stack.peek() - 1;
maxArea = Math.max(maxArea, height * width);
}
if (i != len) {
stack.push(i);
}
}
return maxArea;
}- run time: O(n)
A Wrong DP Solution
I once came to a wrong DP solution for this question:
- for bar 1 ~ n:
- left[i] = height[i] > height[i – 1] ? i : left[i – 1]
- for bar n – 1: 0:
- right[i] = height[i] > height[i + 1] ? i : right[i + 1]
The following diagram illustrated why it is incorrect:
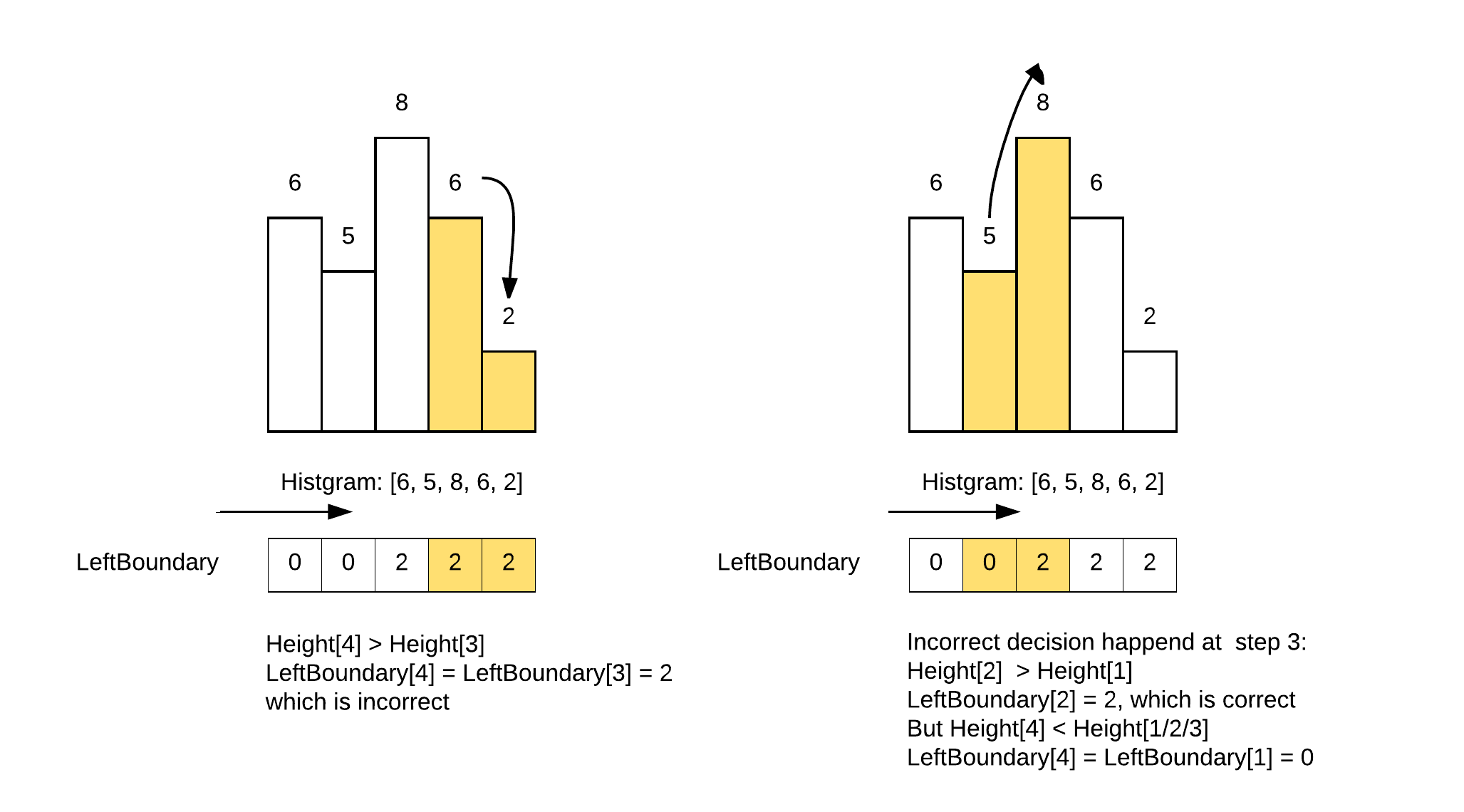
The thing I learned was: always be careful with DP solutions : )