Regular Expression Matching Problem
Implement regular expression matching with support for ‘.’ and ‘*’.
'.' Matches any single character.
'*' Matches zero or more of the preceding element.
The matching should cover the entire input string (not partial).
The function prototype should be:
bool isMatch(const char *s, const char *p)
Some examples:
isMatch("aa","a") ? false
isMatch("aa","aa") ? true
isMatch("aaa","aa") ? false
isMatch("aa", "a*") ? true
isMatch("aa", ".*") ? true
isMatch("ab", ".*") ? true
isMatch("aab", "c*a*b") ? trueReduction Transition Function
B[j] is a regular character
match[i + 1][j + 1] = A[i] == B[j] && match[i][j]
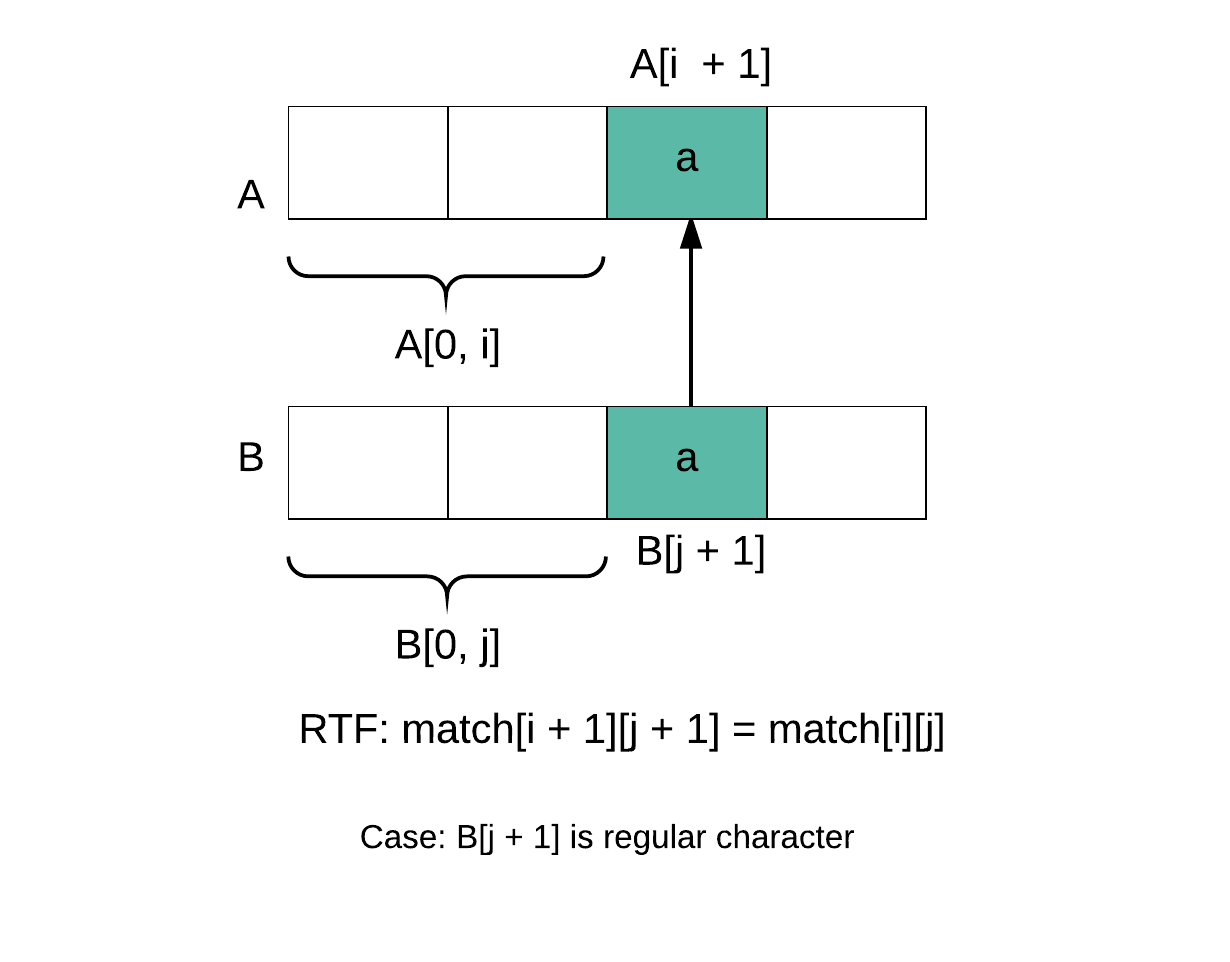
B[j] is ‘.’
match[i + 1][j + 1] = A[i] == B[j] && match[i][j]
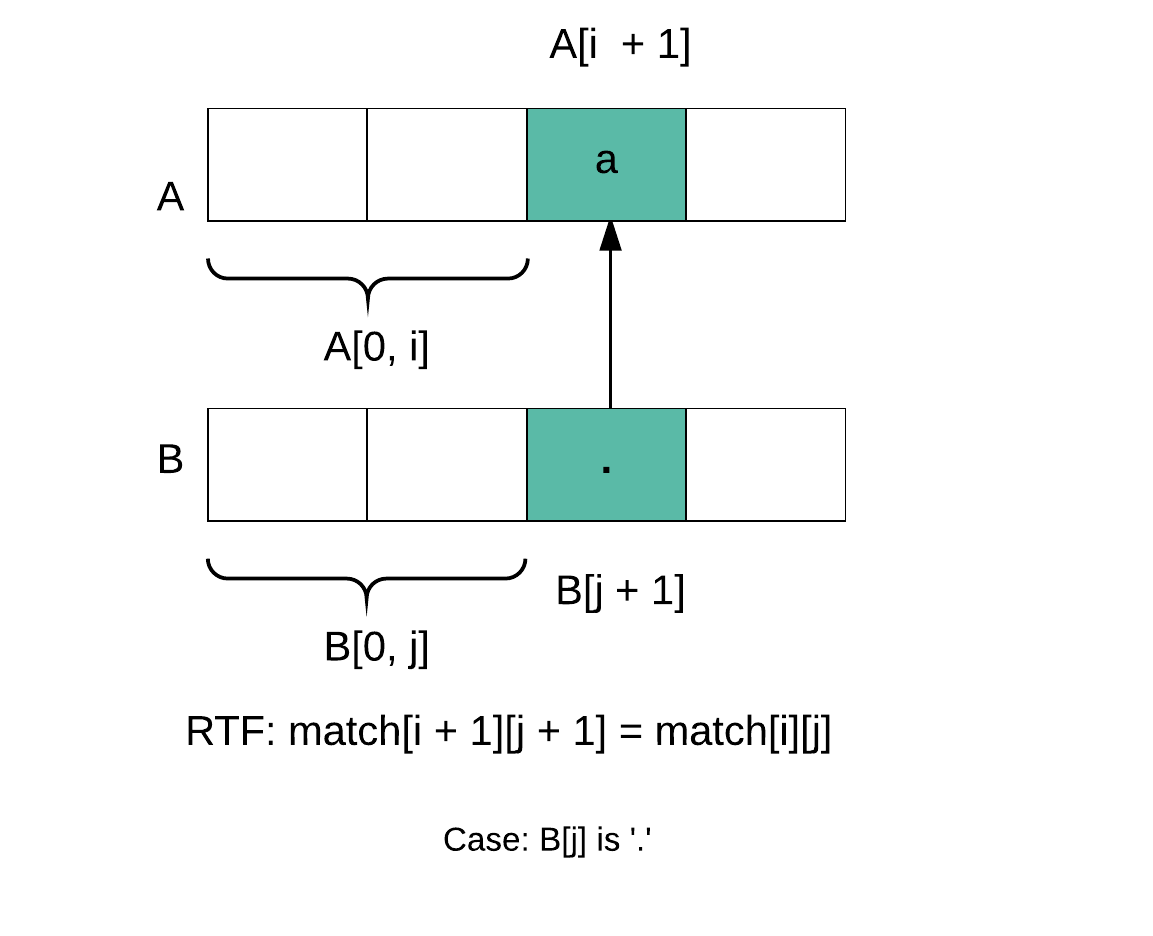
B[j] is ‘*’
There are three different cases:
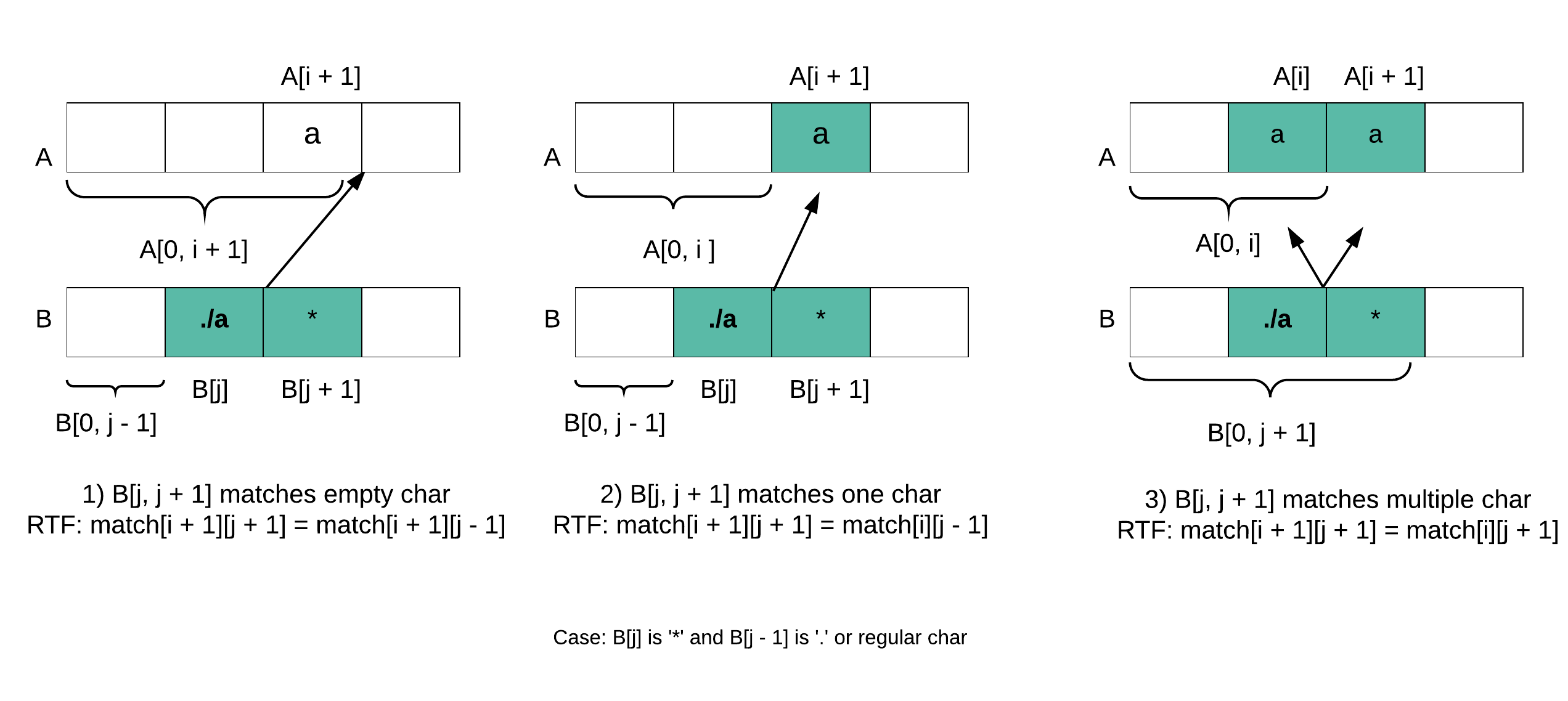
B[j] matches zero preceding element
match[i + 1][j + 1] = match[i + 1][j – 1]
B[j] matches one preceding element
match[i + 1][j + 1] = (B[j – 1] == ‘.’ || B[j – 1] == A[j]) && match[i + 1][j]
The preceding element has to be ‘.’ or the same as B[j].
B[j] matches multiple preceding element
match[i + 1][j + 1] = (B[j – 1] == ‘.’ || B[j – 1] == A[j]) && match[i][j + 1]
When matching with multiple elements, preceding element has to be ‘.’ or the same as B[j].
Implementation
The following diagram illustrate how this algorithm works with an matrix:

Initiate first row
How to get the correct value for the first row? match[0, i] means: whether B[0, i] matches an empty string. Since only * can match with zero string, this question is another DP solution, the RTF is:
match[0][i + 1] = (B[i] == ‘*’ && match[0][i – 1])
Where match[0][i – 1] indicates whether B[0, i – 2] matches empty string.
The following is the implementation of the algorithm:
public boolean isMatch(String s, String p) {
int len1 = s.length();
int len2 = p.length();
boolean[][] match = new boolean[len1 + 1][len2 + 1];
match[0][0] = true;
for (int i = 0; i < len2; i++) {
if (p.charAt(i) == '*' && match[0][i - 1]) {
match[0][i + 1] = true;
}
}
for (int i = 0; i < len1; i++) {
for (int j = 0; j < len2; j++) {
// p[j] is '.'.
if (p.charAt(j) == '.') {
match[i + 1][j + 1] = match[i][j];
}
// P[j] is a regular char.
if (p.charAt(j) == s.charAt(i)) {
match[i + 1][j + 1] = match[i][j];
}
if (p.charAt(j) == '*') {
// preceding char does not match, count as empty.
if (p.charAt(j - 1) != '.' && p.charAt(j - 1) != s.charAt(i)) {
match[i + 1][j + 1] = match[i + 1][j - 1];
} else {
// match[i + 1][j]: match one char.
// match[i][j + 1]: match multiple char.
// match[i + 1][j - 1]: match empty char.
match[i + 1][j + 1] = match[i + 1][j] || match[i][j + 1] || match[i + 1][j - 1];
}
}
}
}
return match[len1][len2];
}